Trong công tác toán lớp 10 đại số, giao hội là sự giản dị và đơn giản tuy nhiên là nền tảng nhưng mà bất kể học viên nào thì cũng nên nắm vững nhằm áp dụng mang lại những nội dung tiếp theo sau.
Mục lục
I. Tập hợp
1, Khái niệm tập luyện hợp
2, Tập con cái và giao hội vày nhau
II. Các quy tắc toán tập luyện hợp
1, Giao của nhì tập luyện hợp
2, Hợp của nhì tập luyện hợp
3, Hiệu và phần bù của nhì tập luyện hợp
III. Các giao hội số
Để hiểu một những cụ thể nhất về giao hội, thầy Lưu Huy Thưởng (giáo viên môn Toán bên trên Hệ thống giáo dục và đào tạo HOCMAI) vẫn chứng thật cho những em học viên về thế nào là là giao hội, những quy tắc toán giao hội và những giao hội số canh ty học viên thực hiện bài xích tập luyện một cơ hội hiệu suất cao.
-
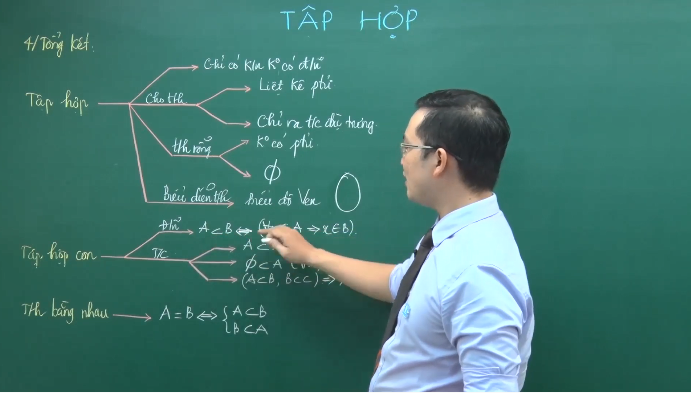
1, Khái niệm tập luyện hợpa, Khái niệm tập luyện hợp
- Khái niệm giao hội bao hàm thành phần sở hữu cộng đồng một hoặc một vài ba đặc thù nào là bại.Ví dụ: “Tập ăn ý những số bất ngờ phân tách không còn mang lại 3 và nhỏ rộng lớn 20” : Là giao hội những số bất ngờ vừa lòng 2 đặc thù một vừa hai phải phân tách không còn mang lại 3 và nhỏ rộng lớn đôi mươi.Kí hiệu: Tập ăn ý được kí hiệu vày vần âm in hoa.Các thành phần được ghi nhập nhì vệt ngoặc nhọn { }, cách nhau chừng vày vệt , hoặc ;Ví dụ: a là thành phần nằm trong giao hội X kí hiệu là a ∈ X b, Cách cho 1 tập luyện hợp Một giao hội rất có thể được xác lập bằng phương pháp đã cho thấy đặc thù đặc thù cho những thành phần của chính nó. Vậy tớ rất có thể xác lập một giao hội vày 2 cơ hội sau:
-
-
- Liệt kê những thành phần : C = {phần tử}
-
Ví dụ: C = {4, 2, 1, 3}
-
-
- Chỉ rời khỏi đặc thù đặc thù của những phần tử
-
Chỉ rõ ràng đặc thù đặc thù của những thành phần canh ty tóm gọn cộc gọn gàng những giao hội dài
Ví dụ: Tập ăn ý những số bất ngờ nhỏ rộng lớn 4
c, Tập rỗng
Khái niệm: Tập trống rỗng là giao hội không tồn tại thành phần nào
Kí hiệu:

Ví dụ:

2, Tập con cái và giao hội vày nhau
a, Tập con
Cho 2 thành phần A và B, từng thành phần nằm trong A đều nằm trong B khi bại A là tập luyện con cái của B.
Kí hiệu: A⊂B
Tính chất:
– Nếu A là con cái của B, B là con cái của C thì A là con cái của C
– Mọi giao hội đều là tập luyện con cái của nó, tức thị tập luyện A là con cái của tập luyện A, tập luyện B là con cái của tập luyện B
– Tập trống rỗng là tập luyện con cái của từng tập luyện hợp
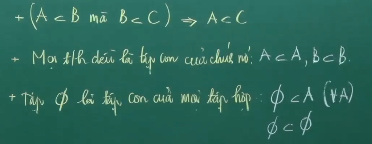
b, Tập ăn ý vày nhau: A là con cái của tập luyện A, B là con cái của tập luyện B thì tớ bảo rằng tớ bảo rằng giao hội A vày giao hội B hoặc tớ bảo rằng từng thành phần nằm trong giao hội A đều nằm trong giao hội B và ngược lại.
Kí hiệu: A=B⇔ (A⊂B) và (B⊂A)

Các quy tắc toán tập luyện hợp
1, Giao của nhì tập luyện hợpKhái niệm: Tập ăn ý C bao gồm những thành phần vừa thuộc A, vừa thuộc B được gọi là giao của A và B.
Ký hiệu

Ví dụ
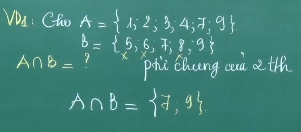
2, Hợp của nhì tập luyện hợp
Khái niệm: Tập ăn ý C bao gồm những thành phần một vừa hai phải nằm trong A hoặc một vừa hai phải nằm trong B được gọi là hợp của A và B.
Ký hiệu
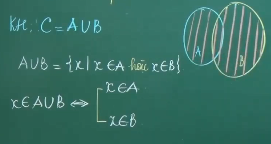
Ví dụ
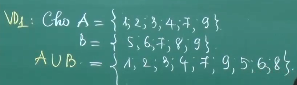
3, Hiệu và phần bù của nhì tập luyện hợp
a, Hiệu của nhì tập luyện hợp
Khái niệm: Tập ăn ý C bao gồm những thành phần một vừa hai phải nằm trong A nhưng không nằm trong B được gọi là hiệu của A và B.
Ký hiệu
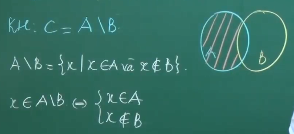
Ví dụ
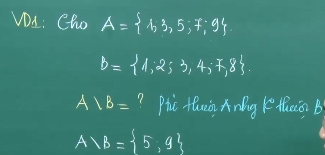
b, Phần bù của nhì tập luyện hợp
Khái niệm: Khi B là con cái của A thì A\B gọi là phần bù của B nhập A.
Ký hiệu

Ví dụ
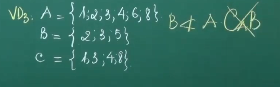
Các giao hội số
Tập ăn ý những số bất ngờ N,N*
Tập ăn ý những số nguyên vẹn Z
Tập ăn ý những số hữu tỷ Q
Tập ăn ý những số thực ℝ
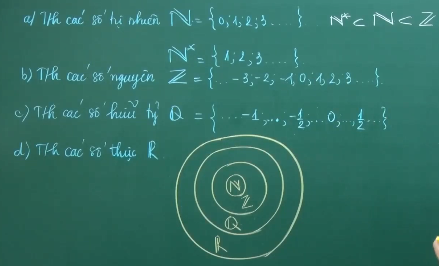
Một số tập luyện con cái của tập luyện số thực ℝ

-
